交互式在线版本:

训练参数子集

在训练神经网络时，有时固定网络的一些参数，同时更新其他参数会很有用。这通常被称为“不可训练变量”或“层冻结”。

在典型的神经网络训练中，参数通过计算梯度并通过诸如 SGD 或 ADAM 之类的优化器计算更新来更新。然后将更新应用于参数，并重复该过程直到收敛。

因此，为了在 JAX 中实现“层冻结”或“不可训练变量”，我们只需要不计算和应用我们网络某些参数的更新。

在 JAX 中，计算梯度和将更新应用于参数完全在您作为用户的控制之下。JAX 的自动微分机制允许您计算关于函数任何位置参数的梯度。

在 Haiku（和其他 NN 库）中，通常将您的参数作为单个位置参数传递给您的函数（例如 grads = jax.grad(loss_fn)(params, ...)）。

为了支持对参数子集求梯度，我们需要允许用户将其参数拆分为两个位置参数，以便他们可以计算关于其参数子集的梯度（例如 trainable_params_grads = jax.grad(loss_fn)(trainable_params, non_trainable_params, ...)）。

Haiku 附带了一些实用程序，可以更轻松地操作参数字典，以便拆分为这些可训练/不可训练的集合，以及将您的参数重新组合成单个字典。

我们将逐步介绍如何使用简单的 MLP 来完成此操作，并教导它恒等函数。

import haiku as hk
import jax
import jax.numpy as jnp
import numpy as np

我们网络的前向传播是一个标准的 MLP。我们想要调整这个 MLP 的参数，使其计算恒等式。也就是说 forward([[1.0], [2.0], [3.0]) == [1, 2, 3]。我们将对最多 10 个数字执行此操作。

我们的网络开始时是随机初始化的，因此最初的结果没有太多意义

num_classes = 10

def f(x):
  return hk.nets.MLP([300, 100, num_classes])(x)

f = hk.transform(f)

def test(params, num_classes=num_classes):
  x = np.arange(num_classes).reshape([num_classes, 1]).astype(np.float32)
  y = jnp.argmax(f.apply(params, None, x), axis=-1)
  for x, y in zip(x, y):
    print(x, "->", y)

rng = jax.random.PRNGKey(42)
x = np.zeros([num_classes, 1])
params = f.init(rng, x)

print("before training")
test(params)

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
/tmp/haiku-docs-env/lib/python3.8/site-packages/jax/_src/lax/lax.py:6271: UserWarning: Explicitly requested dtype float64 requested in zeros is not available, and will be truncated to dtype float32. To enable more dtypes, set the jax_enable_x64 configuration option or the JAX_ENABLE_X64 shell environment variable. See https://github.com/google/jax#current-gotchas for more.
  warnings.warn(msg.format(dtype, fun_name , truncated_dtype))

before training
[0.] -> 0
[1.] -> 3
[2.] -> 3
[3.] -> 3
[4.] -> 3
[5.] -> 3
[6.] -> 3
[7.] -> 3
[8.] -> 3
[9.] -> 3

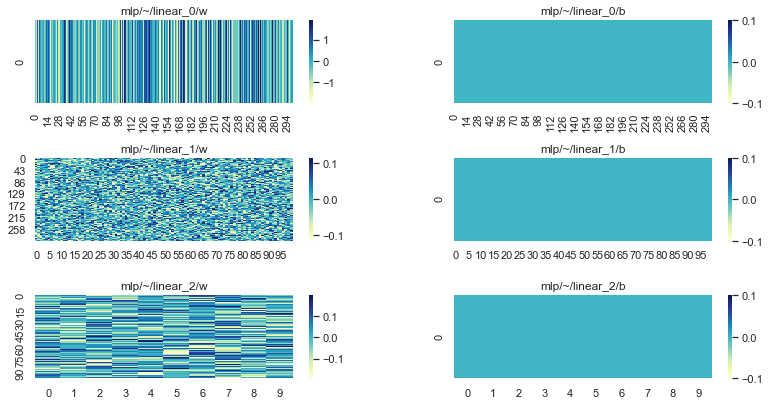
可视化我们的参数很有用，这样我们可以将其与最终状态进行比较

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()

def plot_params(params):
  fig, axs = plt.subplots(ncols=2, nrows=3)
  fig.tight_layout()
  fig.set_figwidth(12)
  fig.set_figheight(6)
  for row, module in enumerate(sorted(params)):
    ax = axs[row][0]
    sns.heatmap(params[module]["w"], cmap="YlGnBu", ax=ax)
    ax.title.set_text(f"{module}/w")

    ax = axs[row][1]
    b = np.expand_dims(params[module]["b"], axis=0)
    sns.heatmap(b, cmap="YlGnBu", ax=ax)
    ax.title.set_text(f"{module}/b")

plot_params(params)

为了训练我们的网络，我们将创建一些简单的合成数据批次

def dataset(*, batch_size, num_records):
  for _ in range(num_records):
    y = np.arange(num_classes)
    y = np.random.permutation(y)[:batch_size]
    x = y.reshape([batch_size, 1]).astype(np.float32)
    yield x, y

for x, y in dataset(batch_size=4, num_records=5):
  print("x :=", x.tolist(), "y :=", y)

x := [[0.0], [8.0], [7.0], [1.0]] y := [0 8 7 1]
x := [[6.0], [7.0], [0.0], [9.0]] y := [6 7 0 9]
x := [[4.0], [0.0], [9.0], [6.0]] y := [4 0 9 6]
x := [[0.0], [4.0], [6.0], [5.0]] y := [0 4 6 5]
x := [[4.0], [3.0], [0.0], [5.0]] y := [4 3 0 5]

现在是有趣的部分。假设我们只想更新 MLP 的第一层和最后一层的参数。

最简单和最有效的方法是将我们的参数划分为两组：“可训练”和“不可训练”。Haiku 提供了一个方便的函数 hk.data_structures.partition(..) 来执行此操作

# Partition our params into trainable and non trainable explicitly.
trainable_params, non_trainable_params = hk.data_structures.partition(
    lambda m, n, p: m != "mlp/~/linear_1", params)

print("trainable:", list(trainable_params))
print("non_trainable:", list(non_trainable_params))

trainable: ['mlp/~/linear_0', 'mlp/~/linear_2']
non_trainable: ['mlp/~/linear_1']

我们拆分参数的原因是这允许我们将它们作为单独的位置参数传递给我们的损失函数。

在 JAX 中，梯度是相对于位置参数计算的。通过将我们的参数拆分为两组，我们可以仅针对其中一个位置参数计算梯度。然后，我们可以使用这些梯度来更新我们参数的子集。

最后一块拼图是我们需要在调用应用函数之前将我们的“可训练”和“不可训练”参数组合在一起。同样，Haiku 提供了 hk.data_structures.merge(..) 以使其变得容易

def loss_fn(trainable_params, non_trainable_params, images, labels):
  # NOTE: We need to combine trainable and non trainable before calling apply.
  params = hk.data_structures.merge(trainable_params, non_trainable_params)

  # NOTE: From here on this is a standard softmax cross entropy loss.
  logits = f.apply(params, None, images)
  labels = jax.nn.one_hot(labels, logits.shape[-1])
  return -jnp.sum(labels * jax.nn.log_softmax(logits)) / labels.shape[0]

def sgd_step(params, grads, *, lr):
  return jax.tree_util.tree_map(lambda p, g: p - g * lr, params, grads)

def train_step(trainable_params, non_trainable_params, x, y):
  # NOTE: We will only compute gradients wrt `trainable_params`.
  trainable_params_grads = jax.grad(loss_fn)(trainable_params,
                                             non_trainable_params, x, y)

  # NOTE: We are only updating `trainable_params`.
  trainable_params = sgd_step(trainable_params, trainable_params_grads, lr=0.1)
  return trainable_params

train_step = jax.jit(train_step)

for x, y in dataset(batch_size=num_classes, num_records=10000):
  # NOTE: In our training loop only our trainable parameters are updated.
  trainable_params = train_step(trainable_params, non_trainable_params, x, y)

我们可以看到，即使我们只训练了参数的子集，我们的 NN 也能够学习这个简单的函数

# Merge params again for inference.
params = hk.data_structures.merge(trainable_params, non_trainable_params)

print("after training")
test(params)

after training
[0.] -> 0
[1.] -> 1
[2.] -> 2
[3.] -> 3
[4.] -> 4
[5.] -> 5
[6.] -> 6
[7.] -> 7
[8.] -> 8
[9.] -> 9

当然，它不够聪明，无法推广到分布外的输入

test(params, num_classes=num_classes+10)

[0.] -> 0
[1.] -> 1
[2.] -> 2
[3.] -> 3
[4.] -> 4
[5.] -> 5
[6.] -> 6
[7.] -> 7
[8.] -> 8
[9.] -> 9
[10.] -> 9
[11.] -> 9
[12.] -> 9
[13.] -> 9
[14.] -> 9
[15.] -> 9
[16.] -> 9
[17.] -> 9
[18.] -> 9
[19.] -> 9

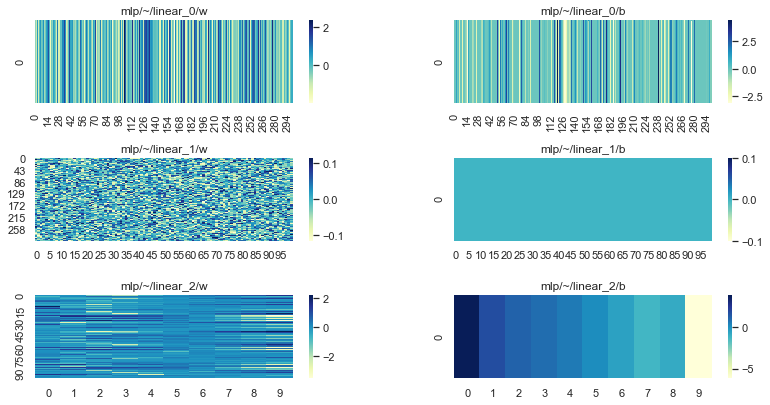
查看我们的参数，我们可以看到 linear_1 仍然处于其初始状态（随机初始化的权重矩阵和零初始化的偏置）

plot_params(params)

使用 Optax 冻结层

或者，Optax 用户可以使用 `optax.multi_transform <https://optax.readthedocs.io/en/latest/api.html#optax.multi_transform>`__ 来固定参数。用户可以在此处阅读更多内容。